
簡諧運動專用HD執(zhí)行元件CSF-3B-50-1U-CC-SP(或簡諧振動、諧振‵SHM(Simple Harmonic Motion))既是最基本也是最簡單的一種機械振動。當某物體進行簡諧運動時,物體所受的力跟位移成正比,并且力總是指向平衡位置。
物體的位移與時間的關系遵從正弦函數(shù)的規(guī)律(即它的振動圖像是一條正弦曲線)的振動叫簡諧運動。
在阻力作用下的震動,當阻力大小可以忽略時,可以說是簡諧運動。
簡諧運動專用HD執(zhí)行元件CSF-3B-50-1U-CC-SP(振動過程中受到阻力的作用,振幅逐漸減小,能量逐漸損失,直至振動停止。但在整個過程中震動的頻率不變。
振動方程:x=Αsin(ωt+φ)
將一個有孔小球體與一個彈簧連在一起,將一個極為光滑的水平桿穿入小球體,使球體可以在水平桿上左右滑動,而球體與水平桿的摩擦力小得可以忽略不計。將彈簧的一端固定住,彈簧的整體質(zhì)量要比球體質(zhì)量小得多,這樣彈簧本身質(zhì)量也可以忽略不計。這個系統(tǒng)便是一個彈簧振子。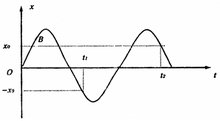
簡諧運動專用HD執(zhí)行元件CSF-3B-50-1U-CC-SP(彈簧振子系統(tǒng)在平衡狀態(tài)下,彈簧沒有形變,振子(小球體)在平衡位置保持靜止。若把振子拉過平衡位置,到達幅度,再松開,彈簧則會將振子向平衡位置收回。在收回的過程中,彈簧的勢能轉換為振子的動能,勢能在降低的同時,動能在增加。當振子到達平衡位置時,振子所積累的動能又迫使振子越過平衡位置,繼續(xù)向同樣的方向移動。但因已越過彈簧振子系統(tǒng)的平衡位置,所以這時彈簧開始對振子向相反方向施加力。動能轉作勢能,動能降低,勢能上升,直至到達離平衡位置幅度的距離。這時振子所有的動能被轉化為勢能,振子速度為零,停止運動。勢能又迫使振子移回平衡位置,在移動過程中,勢能轉為動能,因而再次越過平衡位置,重復這個過程。在沒有任何其他力影響的完美的條件下,這個彈簧振子系統(tǒng)會在兩個幅度點間不停地做往返運動。 彈簧振子的固有周期和固有頻率與彈簧勁度系數(shù)和振子質(zhì)量有關,與振幅大小無關。
回復力的定義:振子受迫使它回復平衡位置的力,是合外力平行于速度方向上的分力。
如果用F表示物體受到的回復力,用x表示小球?qū)τ谄胶馕恢玫奈灰疲鶕?jù)胡克定律,F(xiàn)和x成正比,它們之間的關系可用下式來表示:
F = - kx
式中的k是勁度系數(shù),負號的意思是:回復力的方向總跟物體位移的方向相反。負號只代表方向,不代表數(shù)值正負。
一般簡諧運動周期:T=2π√(m/k). 其中m為振子質(zhì)量,k為振動系統(tǒng)的回復力系數(shù)。
對于單擺運動,其周期T=2π√(L/g) (π為圓周率 √為根號 ) 由此可推出g=(4π^2×L)/(T^2) 據(jù)此可利用實驗求某地的重力加速度,也可以測得擺長L=(T^2×g)/4π。
T與振幅(a<5度)和擺球質(zhì)量無關。
當偏角a<10度時 sina≈a=弧(軌跡)/L(半徑)≈x/L;F回=-mg/Lx
根據(jù)牛頓定律,F(xiàn)=ma,運動物體的加速度總跟物體所受的合力的大小成正比,并且跟合力的方向相同。
振幅、周期和頻率
簡諧運動的頻率(或周期)跟振幅沒有關系。
物體的振動頻率本身的性質(zhì)決定,所以又叫固有頻率。